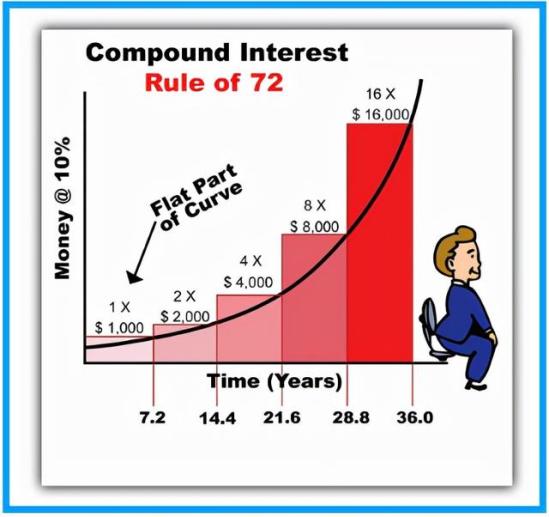
72法则

72法则是估算任何增长率影响的一个很好的心算捷径，从快速的财务计算到人口估算。 这个公式:

翻倍的时间= 72 /利率

这个公式对于财务评估和理解复利的性质是有用的。

例子:

在6%的利率下，你的钱需要72/6或12年才能翻倍。

要在10年内让你的钱翻倍，利率是72/10，也就是7.2%。

如果你国家的GDP以每年3%的速度增长，经济会在72/3或24年内翻倍。

如果你的增长率下滑到2%，它将在36年内翻一番。 如果增长到4%，经济将在18年内翻一番。 考虑到科技发展的速度，缩短你的成长时间可能非常重要。

你也可以用72法则来计算通货膨胀或利息等费用:

如果通货膨胀率从2%上升到3%，你的钱将在24年内贬值一半，而不是36年。

如果大学学费以每年5%的速度增长(这比通货膨胀快)，学费将在72/5或14.4年翻一番。 如果你的信用卡支付15%的利息，你所欠的金额将在72/15或4.8年内翻倍!

72法则说明了为什么在通胀或GDP扩张中1%的“小”差异会对预测模型产生巨大影响。

顺便说一下，72法则适用于任何增长，包括人口。 你能明白为什么3%的人口增长率对规划来说是一个巨大的问题吗? 而不是需要在36年内翻一番，你只有24年，这对于一个国家面对资源消耗，环境问题都是一个巨大考验。一个百分点就削减了12年的缓冲时间。

公式的推导

在一定的利率下翻倍需要多长时间。 可参考另一篇与你财富积累有关的数学知识

让我们从1元开始，因为它很容易使用(确切的值并不重要)。 假设我们有1元和年利率R，一年后我们有:

1 * (1 R)

例如，在10%的利率下，我们有1元*(1 0.1)= 1.10美元在年底。 2年后，我们会

1 * (1 R) * (1 R)

= 1 * (1 R)^2

在10%的利率下，我们有1 * = 1.21在第2年末。 注意我们第一年挣的那一角钱是如何开始自己赚钱的(一分钱)。 明年，我们创造出另一个一角硬币，开始为我们制造一分钱，连同第一个一分钱的少量贡献。 这就是用赚的钱再去赚钱。

这种看似微小的累积增长使复利变得极其强大——爱因斯坦称之为宇宙中最强大的力量之一。

年复一年地延伸，过了N年我们已经

1 * (1 R) N ^

现在，我们需要找出翻倍的时间，也就是2元。 这个方程是:

1 * (1 R)^ n = 2

从R%利率到2需要多少年? 不太难，对吧? 让我们运用数学知识，找到N

1 * (1 R)^ n = 2

(1 R)^ n = 2

ln((1 R)^N) = ln(2)[两边的自然对数]

N * ln(1 R) = .693

N * R = .693[当R较小时, ln(1 R) ~ R]

N = .693 /R

上面有一个小技巧。 我们用一个近似值来表示ln(1 R) = R。它非常接近-即使在R = .25，近似值也有10%的准确性。 当你使用更大的比率，准确性将变得更糟。

现在让我们稍微整理一下公式。 我们想用R放大100倍，使其为整数，即假设利率R=0.03%，则有(r=3)而不是小数(.03)，即我们在右边分子和分母都乘以100:

N = 69.3 / r

最后一步:69.3很好，但不容易被除, 它与 72很近，而且72有很多因数(2、3、4、6、12……)。 所以72法则就是这样来的。